Two circles with centres O and O′ intersect at two points A and B. A line PQ is drawn parallel to OO′ through A(or B) intersecting the circles at P and Q. Find the ratio PQ:OO′.
Answer:
2:1
- Consider the image below:
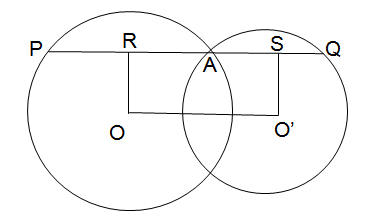
We see that the line drawn at point O perpendicular to OO′ meets the line PQ at a point R.
A similar line drawn at O′ meets PQ at a point S.
Now, PA is a chord, and OR is a line perpendicular to it drawn from the centre of the circle.
We know that a perpendicular drawn from the centre of a circle to a chord bisects the chord. Therefore, OR bisects PA, i.e. PR = RA or PA = 2RA. - Similarly, AQ = 2AS.
We know, PQ = PA + AQ
⇒ PQ = 2RA + 2AS
⇒ PQ = 2(RA + AS)
⇒ PQ = 2OO′ (RA + AS is the same as OO′) - The ratio of PQ:OO′ is 2:1.


